对数函数的定义域概述（解释对数函数的定义域

　　摘要：在数学中，对数函数是指以特定基数为底数，将另一个数作为指数的函数。换句话说，对于给定的基数b，任何正数x，对数函数y=logbx就是使得by=x成立的实数y。对数函数是一种常见的函数形式，它在许多数学和科学问题中都起着重要的作用。

什么是对数函数

 

　　在数学中，对数函数是指以特定基数为底数，将另一个数作为指数的函数。换句话说，对于给定的基数b，任何正数x，对数函数y = logb x 就是使得by = x成立的实数y。

　　对数函数是一种常见的函数形式，它在许多数学和科学问题中都起着重要的作用。

　　

对数函数的定义域

 

　　对数函数的定义域由它的自变量，也就是要求对数的值，所允许的阈值所决定。因此，对数函数的定义域是由它的底数和函数的性质所决定的。

　　对于自然对数函数，其底数为e，该函数的定义域为所有正实数x，即 x > 0。

　　对于特定的底数b，定义域也是所有正实数x，即 x > 0。这是因为对于任何正数x，都可以用指数函数bx表示。

　　

对数函数的取值范围

 

　　对数函数的取值范围由函数的性质所决定。

　　考虑一个常见的例子，即对数函数y = logb x，其中b是正常数且不等于1。

　　当0 < x < 1时，x的对数是负数，因为此时的y是负数。

　　当x = 1时，对数函数的值为0。

　　当x > 1时，x的对数是正数，因为此时的y是正数。

　　因此，对于正数x和正数底数b，对数函数的取值范围是负无穷到正无穷。而对于负数和复数，则没有定义。

　　

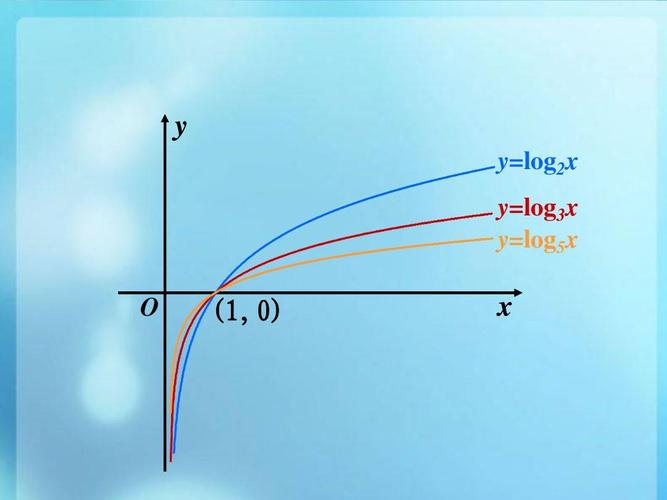
对数函数的图像

 

　　对数函数的图像并不像一般的函数那样光滑和连续。它的图像在x轴的左侧振荡，而在右侧则向上平稳的曲线。

　　以自然对数函数y = ln(x)为例，它的图像是一条单调递增的曲线，在x = 1处有一个最小值0。

　　当我们增加底数b时，函数图像会向左移动或向右移动，而当我们增加或减少函数的系数时，图像则变得更加陡峭或平缓。

　　

对数函数的举例

 

　　考虑以下两个例子。

　　例子1：计算log28。

　　答案：8可以表示为2的多少次方？答案是3，因为23 = 8。因此，log28 = 3。

　　例子2：计算log1010000。

　　答案：10,000可以表示为10的多少次方？答案是4，因为104 = 10,000。因此，log1010000 = 4。

　　在许多数学和科学问题中，对数函数都是非常有用的。有时，对数函数可以被转换为其他类型的函数，以便更好地解决问题。

　　

总结

 

　　对数函数是以一个数为指数的函数，而自然对数和常用对数又是我们常用的对数函数。对于自然对数函数y = ln(x)，它的底数为e，定义域是所有正实数x。

　　它的取值范围是在负无穷到正无穷之间。对于常用对数，它的底数为10，定义域也是所有正实数x，取值范围同样在负无穷到正无穷之间。

　　对数函数在许多领域中都是非常有用的，例如金融投资、科学研究和计算机科学等等。了解对数函数的定义域和取值范围可以帮助我们更好地理解这些方面的问题。