双曲线的实轴和虚轴（解释双曲线的实轴和虚轴

　　摘要：实轴和虚轴是双曲线的重要性质，它们在描述双曲线的对称性、趋近方向以及应用方面起着重要的作用。通过理解双曲线的实轴和虚轴，我们可以更好地理解双曲线的性质和应用，进而进一步探索这种曲线的各种可能性。

双曲线的实轴和虚轴

 

　　双曲线是二元二次方程的一种类型，与圆和椭圆类似，有实轴和虚轴。实轴和虚轴是双曲线的两个重要的属性，在研究双曲线的性质和应用中起着重要的作用。

　　

双曲线的定义

 

　　双曲线是由下列方程所定义的二次曲线：

　　$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

　　其中，a和b都是正实数，也称为双曲线的半轴。

　　

实轴和虚轴的定义

 

　　双曲线有两个轴，分别是实轴和虚轴。实轴是通过两个焦点且垂直于双曲线的直线。虚轴是通过两个焦点且平行于双曲线的直线。

　　在上图中，点F1和F2是焦点，点P是双曲线上的点。实轴是直线F1F2，虚轴是直线AB。当点P位于实轴之上或虚轴之下时，y坐标是正数；当点P位于虚轴之上或实轴之下时，y坐标是负数。

　　

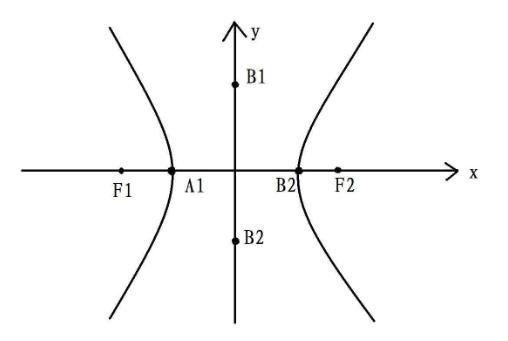
实轴和虚轴的性质

 

　　实轴和虚轴是双曲线的两个重要属性，这些属性可用于描述双曲线的性质。

　　

实轴是对称轴

 

　　双曲线的实轴是一条对称轴，将双曲线沿着实轴折叠后，使得双曲线的两边重合，即可得到原双曲线。

　　

虚轴是渐近线

 

　　虚轴是双曲线的一条渐近线，也就是说，双曲线的曲线趋于虚轴时，与虚轴越来越接近，但永远不会相交。虚轴是双曲线的重要性质，因为它在分析和解决问题时起到了重要的作用。

　　

实轴和虚轴的交点

 

　　实轴和虚轴相交于双曲线的中心点，记为O点。O点是双曲线的对称中心，也是双曲线的焦点之间的中点。

　　

实轴和虚轴的应用

 

　　在数学和物理学中，双曲线是一种重要的数学工具，用于研究各种现象。一些实际应用包括：

　　

椭球坐标系

 

　　椭球坐标系是一种将三维空间中的点表示为椭圆面上的两个坐标和距离的坐标系。这个系统建立在双曲线的性质基础上，其中一个坐标是双曲线的实轴上的投影，另一个坐标是距离，以及双曲线的虚轴上的投影。

　　

焦距

 

　　焦距是一个物体到双曲线焦点之间的距离。在物理学和光学中，焦距是很重要的，因为它可以帮助确定物体成像的位置。

　　

特殊相对论

 

　　相对论是研究物质运动和与之相关的现象的理论。在特殊相对论中，双曲线充当着特殊的角色，因为当一个物体以接近光速的速度运动时，其动量和能量可以用极端双曲线的形式表示，这种双曲线被称为“快速双曲线”。

　　

总结

 

　　实轴和虚轴是双曲线的重要性质，它们在描述双曲线的对称性、趋近方向以及应用方面起着重要的作用。通过理解双曲线的实轴和虚轴，我们可以更好地理解双曲线的性质和应用，进而进一步探索这种曲线的各种可能性。