反比例函数的定义和特点（介绍反比例函数的基

　　摘要：反比例函数是一种特殊的函数，它是由两个变量间成反比例关系所构成的函数。反比例函数作为数学中一种重要的函数类型，在物理学和工程技术中的应用，以及对于数学建模和数据分析等方面都有着重要的意义。

反比例函数的定义

 

　　反比例函数是一种特殊的函数，它是由两个变量间成反比例关系所构成的函数，通常形式为：

　　y = k/x

　　其中 k 是比例常数，x 和 y 是反比例关系的两个变量，而且 x 和 y 不同时为 0。

　　反比例函数可以表示成函数图像，构成一条斜率为负值的直线（在 y 轴和 x 轴上有截距），或一个或多个端点和极值。反比例函数的值域和定义域均为实数域除 0 以外的所有实数。

　　

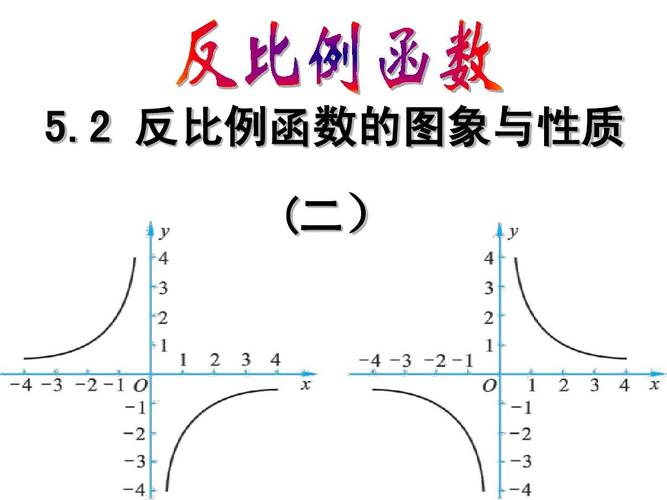
反比例函数的特点

反比例函数的图像

 

　　反比例函数的图像一般为开口向右下或左下的一条直线。由于这个函数在 x 轴上的变化很快，而在 y 轴的变化则较慢，因此其图像是从左下向右上逐渐趋近于 x 轴。（如果 k > 0，函数图像会从右上向左下逐渐趋近于 x 轴。）

　　

反比例函数的定义域和值域

 

　　反比例函数的定义域和值域均为实数域除 0 以外的所有实数。

　　反比例函数的定义域代表的是函数所能接受的正确的变量值，值域是反比例函数所能产生的所有可能的结果值。

　　因此，反比例函数图像在定义域内只存在斜率为正或负的直线，而且因为 y = k/x 在定义域内是无限连续的，所以反比例函数图像不会有间断点。

　　

反比例函数的性质

 

　　反比例函数具有如下性质：

　　反比例函数的幂函数是以 k 的倒数幂为底的指数函数。

　　反比例函数的导数为：

　　y = f(x) = -k/(x^2)

　　其中，y 表示 y 对 x 的导数，而 f(x) 表示反比例函数在任意点 x 处的导数。

　　构建一个反比例函数

　　为了构建一个反比例函数，首先要确定两个变量之间的反比例关系，也就是当一个变量增加时，另一个变量会减小的程度。

　　然后根据反比例关系的定义来确定函数的通用形式，这样就可以得到反比例函数的表达式。最后，对反比例函数进行可视化，并确定函数在定义域内的各种属性（变化方向、端点和极值等）即可。

　　

应用

 

　　反比例函数在应用中有广泛的用途，比如在物理学和工程技术中，反比例函数常用于描述变量之间的关系。

　　例如，摩擦力和物体的速度之间具有反比例关系。由于这种关系，当物体的速度增加时，摩擦力就会下降。反比例函数还可以用于数据拟合或近似检验，以及在预测单个变量在另一个变量固定时的值时进行建模。

　　总之，反比例函数作为数学中一种重要的函数类型，在物理学和工程技术中的应用，以及对于数学建模和数据分析等方面都有着重要的意义。