外接圆的圆心是什么（介绍外接圆的圆心性质和

　　摘要：外接圆是三角形中圆形几何学中的一个重要概念。它是三角形三个顶点的外切圆，只用三个点即可确定一个圆。同时，外接圆具有许多重要的性质，如圆心角是源角的两倍，外接圆的直径等于三角形两边之和，外接圆的半径等于三角形周长的一半。这些性质可以应用到解决一些与三角形相关的问题中。因此，对于理解该概念和其性质的理解非常的重要。

引言

 

　　在初中几何中，我们曾经学习过很多与圆有关的概念，如圆的定义、圆心、半径、弧、圆周角等等，其中有一个很重要的概念叫做“外接圆”，那么什么是外接圆呢？外接圆在圆形几何中是一个至关重要的概念，这篇文章将会详细介绍外接圆的含义、定义及圆心性质。

　　

什么是外接圆？

 

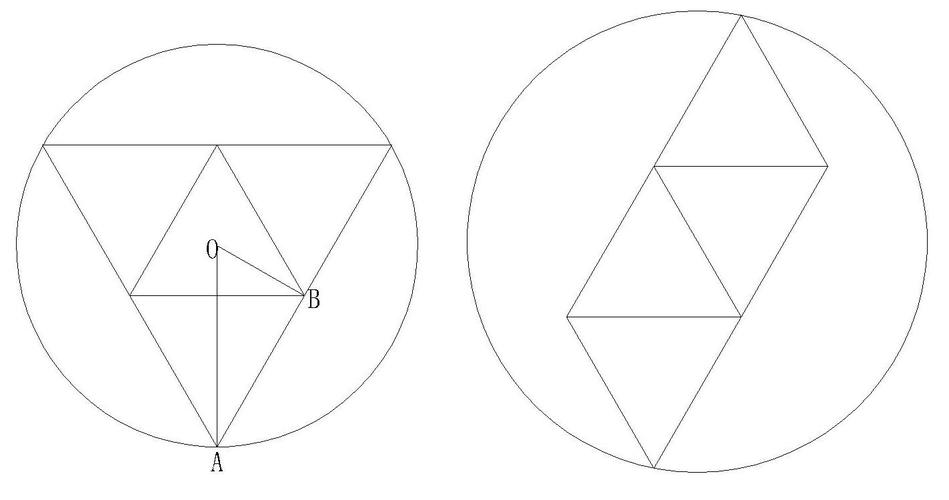
　　外接圆是指一个圆刚好可以通过图形外部的所有顶点，如下图所示：

　　如图所示，外接圆O就是一个圆心在图形外部，半径为r的圆，过A、B、C三个点。当我们把圆完全放置在图形的外面时，圆心的位置和半经就是图形的外接圆的圆心和半径。外接圆的过程可以简化为下面两个步骤：

　　将三角形的顶点O用平移变换，平移到x轴正方向。

　　将三角形O各边在x轴上，得到坐标系中上圆外切三角形O的圆。

　　

外接圆的性质

 

　　现在我们来看一下外接圆的一些重要性质：

　　

1.外接圆的圆心角是源角的两倍

 

　　在三角形ABC中，设外接圆O的半径为R，圆心角∠AOC=2∠BAC，根据圆心角定理，外接圆的圆心角是源角的两倍，所以∠AOC=2∠BAC。

　　我们可以这样证明它：考虑三边的垂线会在圆心处相遇，我们知道圆心角的度数等于圆周角的一半，也等于其对应的弧长的一半。

　　所以OA=OB=OC=R, 垂角OADC=垂角OEBC=垂角OAB=90度。

　　我们遵循以下步骤，就可以得到以下结果：

　　

2.外接圆的直径是三角形两边之和

 

　　在三角形ABC中，设外接圆O的半径为R，∠A、∠B、∠C所对应的弧为a、b、c。我们通过边a的两个端点B和C作垂线，将a分成两段，其长度分别为h1和h2。

　　那么根据正弦定理及三角形面积公式，可以得到：

　　\[\frac{a}{2R}sin\angle A = \frac{h1}{b} = \frac{h2}{c}\]

　　于是我们可以得出：\[\frac{a}{sin\angle A} = \frac{b}{sin\angle B} + \frac{c}{sin\angle C}\]

　　即直径\[\overline{BC}\]等于三角形边长之和。

　　

 

 

　　3.外接圆的半径等于三角形周长的一半

　　

 

　　在三角形ABC中，设外接圆O的半径为R，周长为p=AB+AC+BC。在上述证明中可以用三角形面积公式，即：

　　\[S = \frac{1}{2} a h \sin A\]

　　于是，对于每个对应的边，我们就有：

　　\[b = \frac{2S}{a sin B}, c = \frac{2S}{a sin C}\]

　　代入三边之和的公式，我们就有：

　　\[p = a+b+c=2R(sinA+sinB+sinC) \Rightarrow R = \frac{p}{2(sinA+sinB+sinC)}\]

　　因此，外接圆的半径等于三角形周长的一半除以sine的和，即R＝p/2(sineA＋sineB＋sineC)。

　　综上所述，外接圆的性质有很多，通过这些性质可以应用到求解三角形的问题，是高中数学不可或缺的基础知识之一。

　　

结论

 

　　外接圆是三角形中圆形几何学中的一个重要概念。它是三角形三个顶点的外切圆，只用三个点即可确定一个圆。

　　同时，外接圆具有许多重要的性质，如圆心角是源角的两倍，外接圆的直径等于三角形两边之和，外接圆的半径等于三角形周长的一半。这些性质可以应用到解决一些与三角形相关的问题中。因此，对于理解该概念和其性质的理解非常的重要。