三角形中线的作用揭秘（三角形中线是什么）

　　摘要：中线是三角形中经常出现的一种辅助线，它具有很多重要的性质和应用。通过对中线的理解，我们可以更好地理解三角形的各种性质和定理，也可以更加准确地解决各种三角形相关的问题。因此，在学习三角函数和三角形相关知识的过程中，熟练掌握中线的各种性质和应用，是非常重要的。

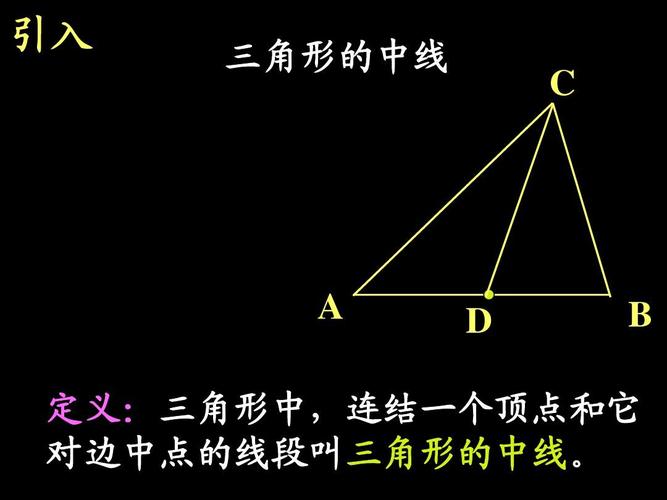
什么是三角形中线

 

　　在三角形中，连接三条边中点的直线称为三角形中线。三角形共有三条中线，分别连接着三个对边的中点，中线也可以视为一个直角三角形的斜边中线。

　　

中线的性质

 

　　1. 连接三角形的两个顶点V1、V2以及V3这些顶点之间的线段，我们称之为第一中线，标记为m1。

　　2. 连接三角形的顶点V2、V3以及V1这些顶点之间的线段，我们称之为第二中线，标记为m2。

　　3. 连接三角形的顶点V3、V1以及V2这些顶点之间的线段，我们称之为第三中线，标记为m3。

　　4. 第一中线m1和第二中线m2相交于三角形的第三个顶点V3的中点M3，横跨同时。

　　5. 第一中线m1和第三中线m3相交于三角形的第二个顶点V2的中点M2，横跨同时。

　　6. 第二中线m2和第三中线m3相交于三角形的第一个顶点V1的中点M1，横跨同时。

　　7. 三角形三个角的平分线在三角形内部相交，交点称为重心G，重心到三角形三个顶点的距离相等，重心到中线的交点距离为中线长的2/3。

　　

中线的作用

 

　　中线作为三角形的一条辅助线，在三角形的各种数学问题中都有它重要的作用，下面我们就来分析一下中线在三角形中的应用。

　　1. 连接三角形的中点可以得到三条中线，而三条中线的交点即是三角形的重心，重心是三角形的一个特殊点，它有很多重要的应用，比如指导重心是质心的做法，还可以用它解决一些面积问题。

　　2. 结合中线定理可以得到三角形的面积公式。中线定理指的是连接三角形两个顶点的中线平行于第三边的这条边的中线长度是其一半，由此可以得到三角形的高，进而求出面积。

　　3. 中线还可以被用来判定三角形的类型。通过寻找中线或是中线长度的比较，我们可以判断三角形是等边三角形、等腰三角形还是普通三角形。

　　4. 中线还可以作为三角形的一个边角的角平分线，对于一些式子复杂的问题，这一性质可以作为求解答案的关键。

　　5. 中线可以被用来证明三角形的各种定理，比如角平分线定理、中垂线定理、直角三角形的证明等。

　　

中线的应用举例

 

　　下面通过具体的问题来展示一下中线的一些应用。

　　1. 已知三角形三边长，求面积

　　三角形三边分别为a，b，c，通过中线定理可以推导出三角形高，h = sqrt((a+b+c) ×(-a+b+c) ×(a-b+c) ×(a+b-c))/2c，进而可以求得三角形面积S = ch/2。

　　2. 已知三角形长度为6、8、10，求面积

　　首先使用中线定理求出第三边长，通过(m1+ 2/m3)= 3/2(10)可得m3 = 7.5，进而可得第三边长为4，随后可以通过海伦公式求得三角形面积S = sqrt(p (p - a)(p - b)(p - c)) = sqrt(9 × 3 × 1 × 7) = 9。

　　3. 证明三角形的垂心定理

　　三角形的垂心定理指的是三角形三条垂线的交点为垂心，该定理可以通过中线来证明。

　　具体来说，假设三角形ABC的中线从A点向BC线段的完全平分点M，连一条垂线，垂足为H，则中线AM和以B、C作顶点的两个小三角形的垂线交于同一点，即H点。同理可证B、C点也是三垂线的交点，从而证明了三角形的垂心定理。

　　

总结

 

　　中线是三角形中经常出现的一种辅助线，它具有很多重要的性质和应用。通过对中线的理解，我们可以更好地理解三角形的各种性质和定理，也可以更加准确地解决各种三角形相关的问题。

　　因此，在学习三角函数和三角形相关知识的过程中，熟练掌握中线的各种性质和应用，是非常重要的。