三角形内心的特点（三角形内心的性质与特点）

　　摘要：三角形内心是一个非常重要的几何中心，它具有很多重要的几何性质和应用价值。熟练掌握三角形内心的特点和性质，能够帮助我们更好地理解数学知识和解决各种问题。

什么是三角形内心

 

　　三角形内心是指一个三角形内部的点，它到三角形的三条边的距离相等，同时还满足内角平分线相交于它。

　　

三角形内心的重要性

 

　　三角形内心具有很多重要的几何性质，被广泛地应用于数学中的各种问题中。

　　

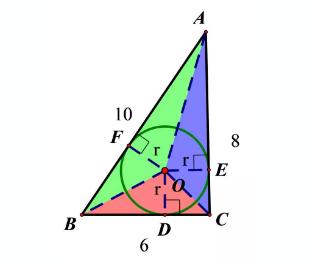
三角形内心的性质与特点

1. 内心到三角形三个顶点的距离相等

 

　　因为内心到三条边的距离相等，而内角平分线又同时是垂直平分线，所以内心到三个顶点的距离也相等。

　　

2. 内角平分线相交于内心

 

　　在三角形内部，从一个顶点引一条内角平分线，它将与另外两个顶点的内角平分线相交于内心。

　　

3. 内心是三角形垂心、重心和外心的共轭点

 

　　三角形的垂心、重心、外心分别是通过三角形三边中点的垂直平分线、三条中线的交点和三角形外接圆的圆心。内心是它们的共轭点，即从三角形内心引的三条角平分线分别交于三边上，那么它们的交点就是垂心、重心和外心。

　　

4. 内心到三角形三边的距离是半周长与面积之比

 

　　假设三角形的三条边分别为a, b, c，半周长为s。那么内心到三角形a边的距离是“半周长s减去a边的长度a，再除以面积S”。

　　

5. 内心是三角形的唯一一点，使得三角形三边的斜率相等

 

　　内心是三角形的唯一一点，使得三角形三边的斜率相等。也就是说，内心到三个顶点连线所构成的直线的斜率相等。

　　

6. 内心是三角形面积最大的点

 

　　在所有到三角形三边距离相等的点中，内心到三条边的距离最小，因此也是使得三角形面积最大的点。

　　

结语

 

　　三角形内心指三个内角的三条角平分线相交于一点，这个点叫做三角形的内心。这个点也是这个三角形内切圆的圆心。三角形内心到三角形三条边的距离相等。

　　三角形内心是一个非常重要的几何中心，它具有很多重要的几何性质和应用价值。熟练掌握三角形内心的特点和性质，能够帮助我们更好地理解数学知识和解决各种问题。