切线怎么证明（证明圆切线的两种基本思路分别

　　摘要：首先来回顾一下切线相关的知识点：切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的性质定理：圆的切线垂直于经过切点的半径。根据这两条定理，我们就可以得到证明圆的切线的一般思路。

　　首先来回顾一下切线相关的知识点：

　　切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。

　　切线的性质定理：圆的切线垂直于经过切点的半径。

　　根据这两条定理，我们就可以得到证明圆的切线的一般思路：

　　1、连半径，证垂直；

　　2、作垂线，证半径。

　　一、若直线L过⊙O上某一点A，证明L是⊙O的切线，只需连OA，证明OA⊥L就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直。

　　例1 如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.

　　求证：EF与⊙O相切.

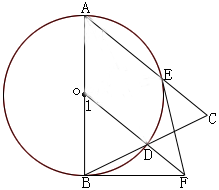
　　分析：点E已经在圆上，连接OE后，OE即为半径，

　　只需要证明OE⊥EF。

　　请看详细思路：

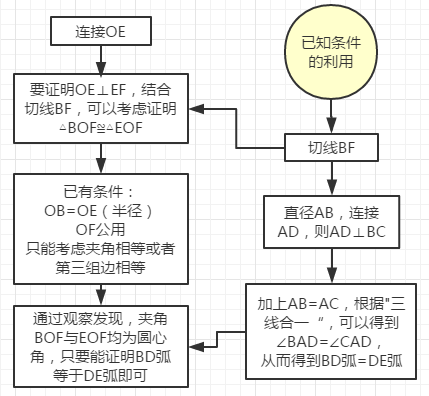
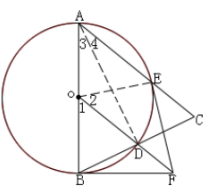
　　说明：此题运用到的知识点：

　　1、直径所对的圆心角是直角；

　　2、等腰三角形三线合一（中线，高，角平分线）；

　　3、同弧所对的圆心角相等，同弧所对的圆周角相等；

　　4、通过“边角边”证明三角形全等。

　　二、若直线L与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥L，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”

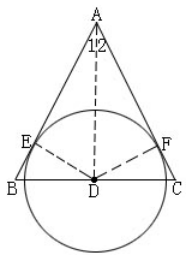
　　例2如图，AB=AC，D为BC中点，⊙D与AB切于E点。

　　求证：AC与⊙D相切。

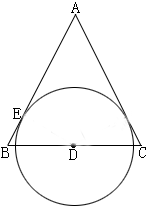
　　分析：AC与圆没有已知公共点，所以，我们就考虑“作垂直；证半径”。

　　请看详细思路：

　　方法一：

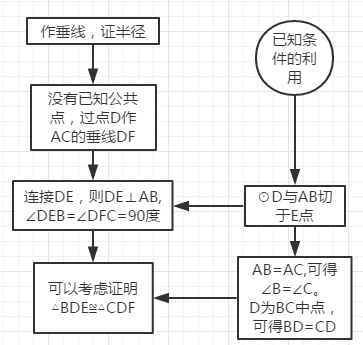
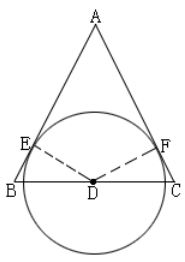
　　说明：此方法运用到的知识点：

　　1、切线的基本性质；

　　2、等腰三角形等边对等角；

　　3、中点；

　　4、通过“角角边”证明两三角形全等。

　　方法二：

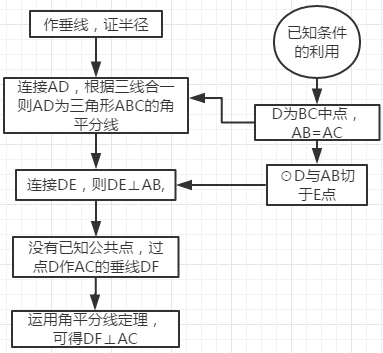
　　说明：此方法运用到的知识点：

　　1、中点，切线；

　　2、等腰三角形三线合一；

　　3、角平分线上的点到角两边的距离（垂线）相等。

　　

小结

 

　　证明圆的切线经常出现在中考题中，因为这类题型可以结合的知识点很多，可简可繁。

　　但是，不论题目怎么变化，基本思路只有上述两种，只要知识点掌握全面，仔细分析，就很容易解决。