转速与角速度的关系（分析转速和角速度之间的

　　摘要：转速和角速度是描述旋转运动的基本物理量，它们之间存在着密切的线性关系。在机械制造、物理实验和动画制作等领域，转速和角速度都是不可或缺的物理量。熟练掌握它们的计算和应用，可以更好地理解和研究旋转运动的特性和状态。

转速和角速度的定义

 

　　在研究转速和角速度的关系之前，我们需要先了解这两个概念的定义。

　　转速是指单位时间内一个物体绕着某一轴线旋转的次数，通常用每分钟转数（rpm）来表示。

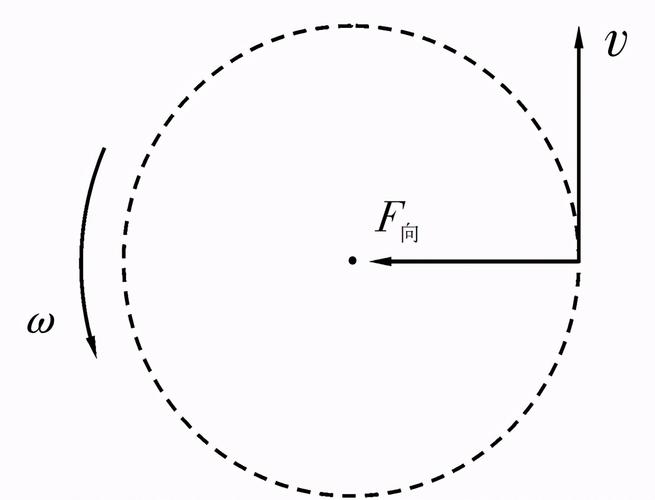
　　而角速度则是指单位时间内一个物体绕着某一轴线旋转的弧长与时间之比，通常用弧度每秒（rad/s）来表示。

　　

转速和角速度的关系

 

　　转速和角速度之间存在着密切的联系。根据定义，可以得出以下公式：

　　角速度 = 转速 x 2π/60

　　这里的2π/60是为了将转速从每分钟转数转换为每秒转数的换算系数。因此，我们可以发现，转速和角速度是线性相关的，其关系由一个常数2π/60确定。

　　举个例子，如果一个物体每分钟转数为600rpm，那么它的角速度就是：

　　600rpm x 2π/60 = 62.83rad/s

　　同样地，如果一个物体的角速度为10rad/s，那么它的转速就是：

　　10rad/s x 60/2π = 95.49rpm

　　从公式中可以看出，转速和角速度之间的关系不但可以直接进行数值计算，而且转换十分方便。这对于很多物理问题的求解都非常有用。

　　

转速和角速度的应用

 

　　在实际应用中，转速和角速度经常被用来描述旋转运动的特性和状态。以下是一些常见的应用场景：

　　1. 机械制造

　　在机械制造领域，转速和角速度常常用于设计和测试机械部件的运动特性。例如，汽车引擎的转速和角速度决定了它的输出功率和燃油效率，而机床的转速和角速度则会直接影响工件的加工精度和表面质量。

　　2. 物理实验

　　在物理实验中，转速和角速度也是重要的物理量之一。例如，用旋转仪器测量物体的惯量和转动惯量时，会涉及到它们的转速和角速度。此外，在惯性导航和天文测量等领域，角速度也是必不可少的物理量。

　　3. 动画制作

　　在电影和游戏制作中，通过对物体的转速和角速度进行精细调整，可以使得图像动画更加逼真和自然。例如，在制作汽车飙车场面时，将车辆的转速和角速度与路面的摩擦系数和路况相结合，可以使得动画效果更加真实。

　　

结论

 

　　转速和角速度是描述旋转运动的基本物理量，它们之间存在着密切的线性关系。在机械制造、物理实验和动画制作等领域，转速和角速度都是不可或缺的物理量。熟练掌握它们的计算和应用，可以更好地理解和研究旋转运动的特性和状态。