函数与反函数的关系是什么（三角之间的4种关系

　　摘要：反三角函数和三角函数互为反函数。一般来说，设函数y=f(x)(x∈A)的值域是C，若找得到一个函数g(y)在每一处g(y)都等于x，这样的函数x=g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数，记作x=f-1(y)。

　　这次我们继续来讨论三角函数和反三角函数的之间的关系和定义域。那你知道有哪些三角函数和反三角函数以及它们之间的关系和定义域吗？

　　首先，我们来看看有哪些三角函数，正弦函数sin α, 余弦函数cos α，正切函数 tan α，余切函数cot α，正割函数sec α,余割函数csc α。

　　接下来，我们来看看有哪些反三角函数，反正弦函数arcsin α，反余弦函数 arccos α,反正切函数arctan α，反正割函数 arcsec α, 反余割函数 arccsc α。

　　继续。我们来看看它们之间的关系。

　　反三角函数和三角函数互为反函数。一般来说，设函数y=f(x)(x∈A)的值域是C，若找得到一个函数g(y)在每一处g(y)都等于x，这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数，记作x=f-1(y) 。

　　反函数x=f -1(y)的定义域是函数y=f(x)的值域，反函数x=f -1(y)的值域是函数y=f(x)的定义域。正函数与反函数的图像是关于y=x对称，最具有代表性的互为反函数就是对数函数与指数函数。

　　有关反函数的内容下次具体讨论。三角函数的之间关系：三角形函数的关系可以用六边形表示，如图1所示。

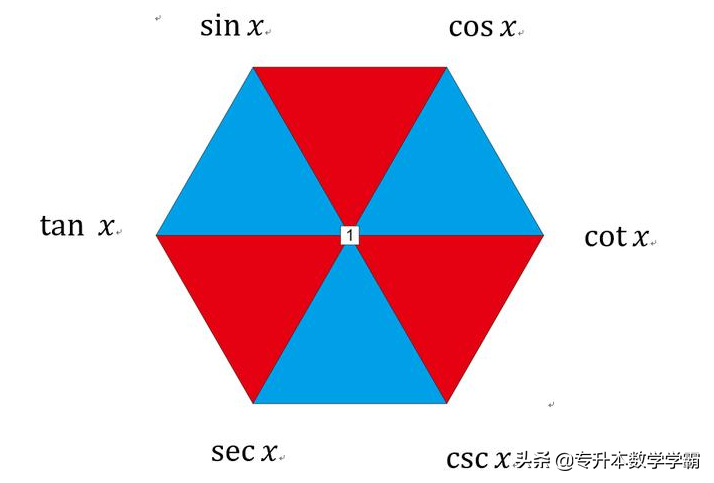
　　图1 三角函数的六边形法则

　　①平方关系，在六边形中，红色区域的倒三角形成平方关系。

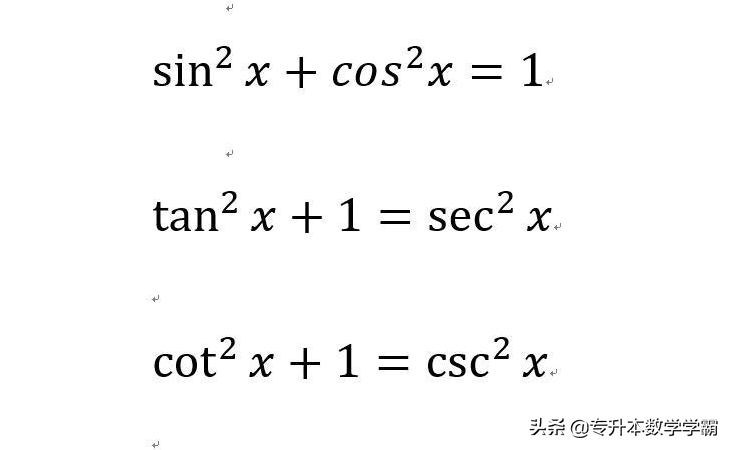
　　图2 平方关系

　　②比值关系，在六边形中，任意一点的值是前面相邻两个函数的比值。

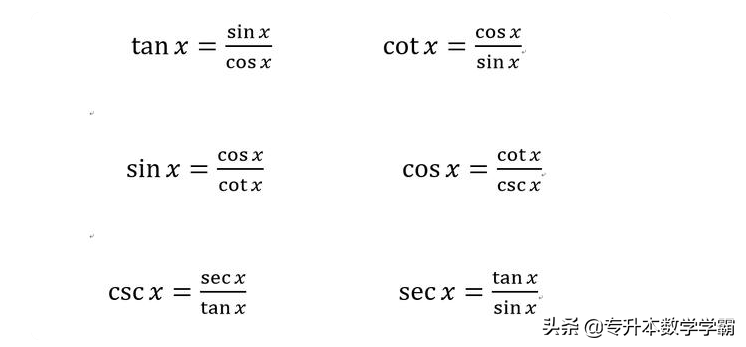
　　图3 比值关系

　　③倒数关系，在六边形中，六边形的对角线的两个三角函数成倒数关系。

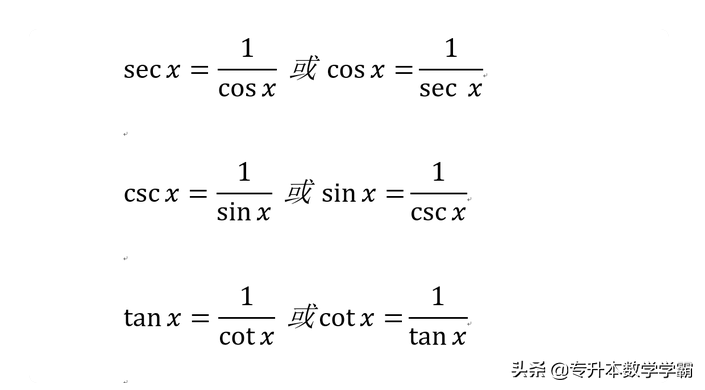
　　图4 倒数关系

　　④ 乘积关系，在六边形中 任意一点的值等于紧挨着这一点的两个端点值 的积

　　图5 乘积关系

　　3.三角函数的定义域：

　　我们一起分别来讨论它们的定义域和值域：

　　①正弦函数sin α的定义域是一切实数R，值域是[-1,1]，其函数图象如图6所示：

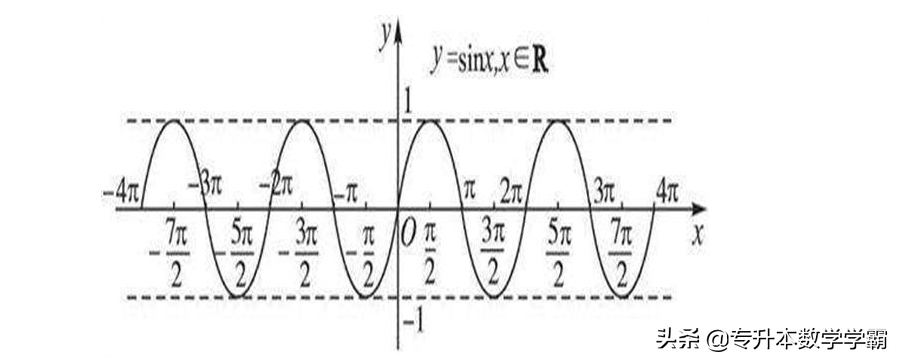
　　图6 正弦函数图像

　　由图象可知，正弦函数是奇函数，周期 T=2π，其对称性是关于原点对称，单调性：单调递增区间：[-π/2±2kπ，π/2±2kπ] ，（K∈Z） ；单调递减区间：[π/2±2kπ，3π/2±2kπ]，（K∈Z）。正弦函数的定义域是反正弦函数的值域，正弦函数的值域是反正弦函数的定义域。

　　②余弦函数cos α的定义域是一切实数R，值域是[-1,1],其函数图象如图7所示：

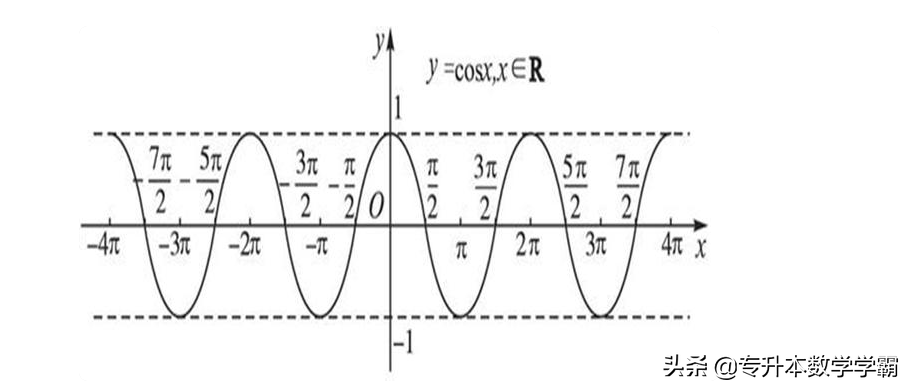
　　图7 余弦函数图像

　　由图象可知，余弦函数是偶函数，周期 T=2π，其对称性是关于y轴对称，单调性：单调递增区间：[π±2kπ，2π±2kπ] ，（K∈Z） 单调递减区间：[0±2kπ，π±2kπ]，（K∈Z）。余弦函数的定义域是反余弦函数的值域，余弦函数的值域是反余弦函数的定义域。

　　③正切函数 tan α的定义域是α ≠ π/2+kπ，（K∈Z），值域是一切实数R，其函数图像如图8所示：

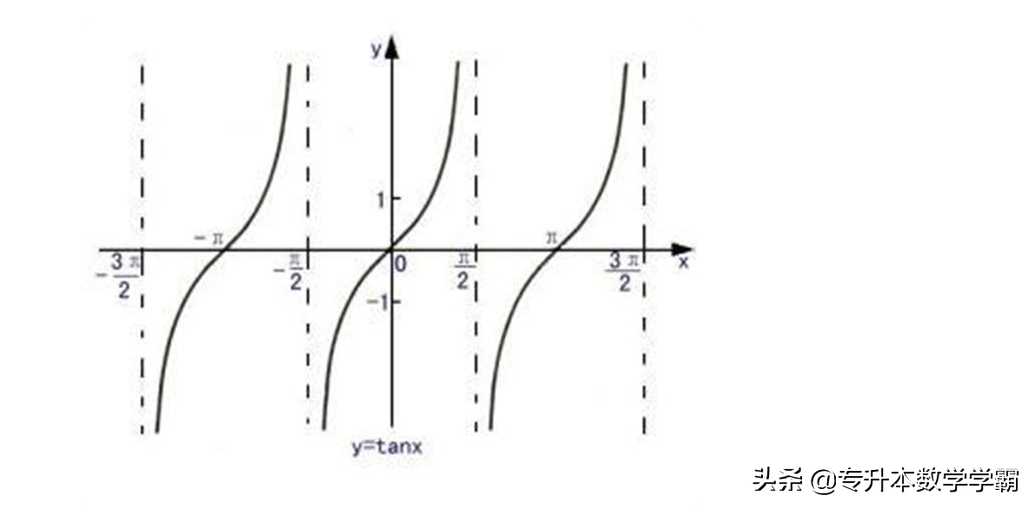
　　图8 正切函数图像

　　由图象可知，正切函数是奇函数，周期 T=π，其对称性是关于原点对称，单调性只有单调递增，单调递增区间为[-π/2±kπ，π/2±kπ] ，（K∈Z），没有单调递减。正切函数的定义域是反正切函数的值域，正切函数的值域是反正切函数的定义域。

　　④ 余切函数cot α的定义域是 α≠kπ，（K∈Z） 值域是一切实数R，其函数图象如图9所示：

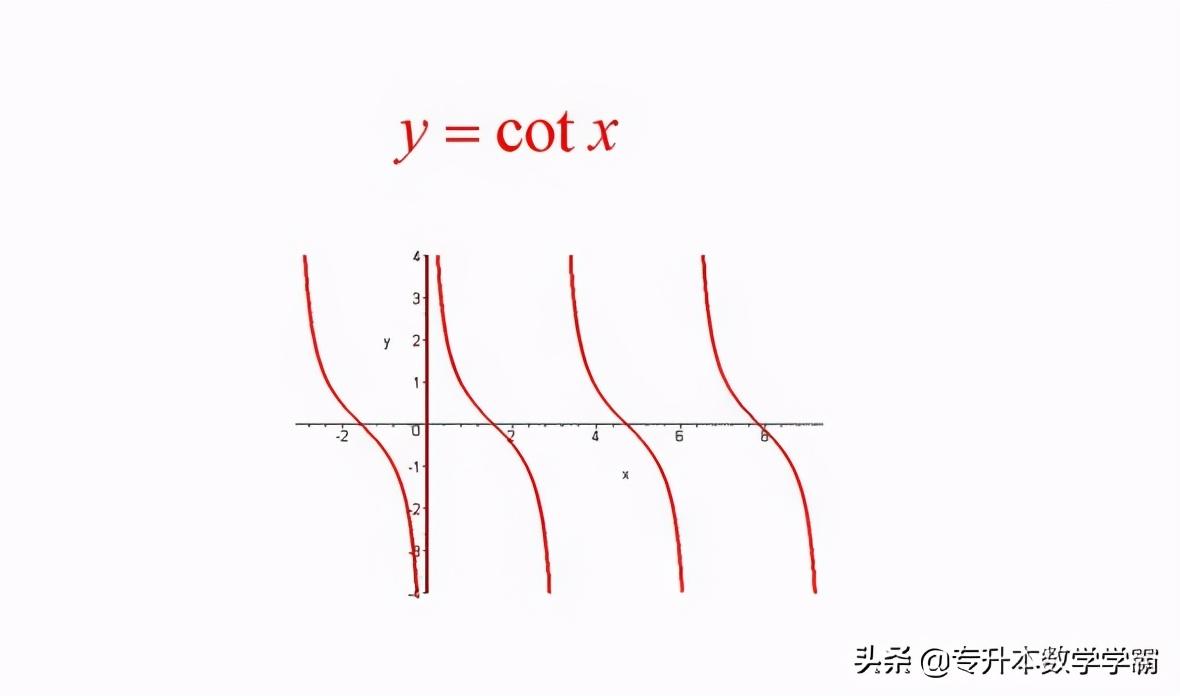
　　图9 余切函数图像

　　由图像可知，余切函数是奇函数，周期 T=π，其对称性是关于原点对称，单调性只有单调递减，单调递减区间为[0±kπ，π±kπ] ，没有单调递增。余切函数的定义域是反余切函数的值域，余切函数的值域是反余切函数的定义域。

　　由于正割函数sec α、余割函数csc α、反正割函数arcsec α、反余割函数arccsc α，专升本数学不考，加上正割函数、余割函数、反正割函数、反余割函数的图像麻烦，就不进行研究了。